15-02 첨도 (kurt / kurtosis)
DataFrame.kurt(axis=None, skipna=None, level=None, numeric_only=None, kwargs)
개요
kurt 메서드는 데이터의 첨도를 구하는 메서드 입니다.
첨도란 데이터의 확률분포가 얼마나 뾰족한지를 나타내는 통계언어입니다.
사용법
기본 사용법
※ 자세한 내용은 아래 예시를 참고 바랍니다.
df.kurt(axis=None, skipna=None, level=None, numeric_only=None, kwargs)
axis : 첨도를 구할 축을 지정합니다
skipna : 결측치를 무시할지 여부 입니다. 기본값은 True로 계산시 무시됩니다.
level : 멀티인덱스의 경우 레벨을 지정할 수 있습니다.
numeric_only : float, int, bool 형식만 포함할지 여부 입니다.
예시
먼저 기본적인 사용법 예시를 위해 13x3짜리 객체를 생성하겠습니다.
l = [-9,-5,-1,-1,0,0,0,0,0,1,1,5,9] # leptokurtic
m = np.random.normal(0,1,13) # mesokurtic
p = [-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6] # Platykurtic
data = {"col1":l,"col2":m,"col3":p}
df = pd.DataFrame(data)
print(df)
>>
col1 col2 col3
0 -9 -0.229079 -6
1 -5 1.809816 -5
2 -1 -0.928193 -4
3 -1 0.483431 -3
4 0 0.821627 -2
5 0 -0.923513 -1
6 0 0.358534 0
7 0 -1.773883 1
8 0 0.061622 2
9 1 -0.538029 3
10 1 0.032397 4
11 5 0.824096 5
12 9 2.082895 6
col1 2.190460
col2 -0.138363
col3 -1.200000
dtype: float64
Process finished with exit code 0
기본적인 사용법
첨도는 정규분포의 m=0 기준으로, 정규분포보다 뾰족한 경우 m>0, 정규분포보다 완만한 경우 m<0으로 값을 계산 할 수 있습니다. m<0 인 경우를 leptokurtic 이라고하고 m=0 인 경우 mesokurtic 이라고하며 m>0 인 경우 platykurtic 이라고 합니다.
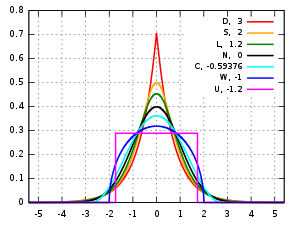
※ 출처 : 위키피디아(https://en.wikipedia.org/wiki/Kurtosis)
col1열의 경우 숫자의 분포가 가장자리가 적고 가운데로 갈수록 많아집니다.
이렇듯 가운데가 뾰족한 경우(정규분포에 비해) 첨도 kurt는 0보다 크게 됩니다.
print(df.kurt())
>>
col1 2.190460
...
...
col2의 경우 numpy를 이용해 평균=0, 표준편차=1 인 정규분포에 근접하는 난수를 출력하였습니다. 따라서 kurt의 값은 0에 근접한 값이 출력됩니다.
print(df.kurt())
>>
...
col2 -0.138363
...
col3의 경우 고른 분포를 그리는 수로 구성되어있으므로 뭉툭한(정규분포에 비해) 경우이므로 kurt의 값은 0보다 작게 됩니다.
print(df.kurt())
>>
...
...
col3 -1.200000'파이썬완전정복-Pandas DataFrame > 15. 통계(심화)' 카테고리의 다른 글
| Pandas DataFrame 15-05 상관계수 (corr / corrwith) (0) | 2022.02.08 |
|---|---|
| Pandas DataFrame 15-04 왜도[비대칭도] (skew) (0) | 2022.02.08 |
| Pandas DataFrame 15-03 표준오차 (sem) (0) | 2022.02.08 |
| Pandas DataFrame 15-01 공분산 (cov) (0) | 2022.02.08 |